22 Mathematical terminology

In analytic geometry, spatial transformations in the 3-dimensional Euclidean space are distinguished into active or alibi transformations, and passive or alias transformations. An active transformation is a transformation which actually changes the physical position of a point, or rigid body, which can be defined in the absence of a coordinate system; whereas a passive transformation is merely a change in the coordinate system in which the object is described. By transformation, mathematicians usually refer to active transformations, while physicists and engineers could mean either. Both types of transformation can be represented by a combination of a translation and a linear transformation.

In measure theory, a property holds almost everywhere if, in a technical sense, the set for which the property holds takes up nearly all possibilities. The notion of "almost everywhere" is a companion notion to the concept of measure zero, and is analogous to the notion of almost surely in probability theory.

In mathematics and computer science, a canonical, normal, or standard form of a mathematical object is a standard way of presenting that object as a mathematical expression. Often, it is one which provides the simplest representation of an object and which allows it to be identified in a unique way. The distinction between "canonical" and "normal" forms varies from subfield to subfield. In most fields, a canonical form specifies a unique representation for every object, while a normal form simply specifies its form, without the requirement of uniqueness.

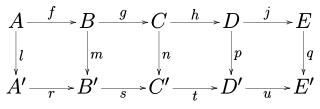
In mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. It is said that commutative diagrams play the role in category theory that equations play in algebra.

In mathematics, a conjecture is a conclusion or a proposition which is suspected to be true due to preliminary supporting evidence, but for which no proof or disproof has yet been found. Some conjectures, such as the Riemann hypothesis or Fermat's Last Theorem, have shaped much of mathematical history as new areas of mathematics are developed in order to prove them.

A definition is a statement of the meaning of a term. Definitions can be classified into two large categories, intensional definitions and extensional definitions. Another important category of definitions is the class of ostensive definitions, which convey the meaning of a term by pointing out examples. A term may have many different senses and multiple meanings, and thus require multiple definitions.

Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or demand that they depend, by some law or rule, on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable in the scope of the experiment in question. In this sense, some common independent variables are time, space, density, mass, fluid flow rate, and previous values of some observed value of interest to predict future values.

Many branches of mathematics study objects of a given type and prove a classification theorem. A common theme is that the classification results in a number of series of objects and a finite number of exceptions — often with desirable properties — that do not fit into any series. These are known as exceptional objects. In many cases, these exceptional objects play a further and important role in the subject. Furthermore, the exceptional objects in one branch of mathematics often relate to the exceptional objects in others.

Formulario Mathematico is a book by Giuseppe Peano which expresses fundamental theorems of mathematics in a symbolic language developed by Peano. The author was assisted by Giovanni Vailati, Mario Pieri, Alessandro Padoa, Giovanni Vacca, Vincenzo Vivanti, Gino Fano and Cesare Burali-Forti.

In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size. There are several different notations used to represent different kinds of inequalities:The notation a < b means that a is less than b. The notation a > b means that a is greater than b.

In mathematics, an invariant is a property of a mathematical object which remains unchanged after operations or transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used. For example, the area of a triangle is an invariant with respect to isometries of the Euclidean plane. The phrases "invariant under" and "invariant to" a transformation are both used. More generally, an invariant with respect to an equivalence relation is a property that is constant on each equivalence class.

In algebraic geometry, a lemniscate is any of several figure-eight or ∞-shaped curves. The word comes from the Latin "lēmniscātus" meaning "decorated with ribbons", from the Greek λημνίσκος meaning "ribbons", or which alternatively may refer to the wool from which the ribbons were made.

Mathematical beauty is the aesthetic pleasure typically derived from the abstractness, purity, simplicity, depth or orderliness of mathematics.Mathematicians often express this pleasure by describing mathematics as beautiful. They might also describe mathematics as an art form or, at a minimum, as a creative activity. Comparisons are often made with music and poetry.

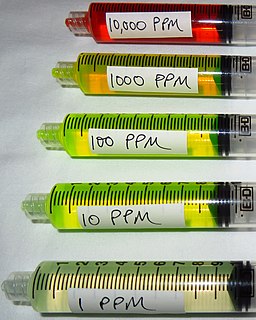
In science and engineering, the parts-per notation is a set of pseudo-units to describe small values of miscellaneous dimensionless quantities, e.g. mole fraction or mass fraction. Since these fractions are quantity-per-quantity measures, they are pure numbers with no associated units of measurement. Commonly used are parts-per-million, parts-per-billion, parts-per-trillion and parts-per-quadrillion. This notation is not part of the International System of Units (SI) system and its meaning is ambiguous.

In mathematics, a pathological object is one which possesses deviant, irregular, or counterintuitive property, in such a way that distinguishes it from what is conceived as a typical object in the same category. The opposite of pathological is well-behaved.

A mathematical proof is an inferential argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning which establish logical certainty, to be distinguished from empirical arguments or non-exhaustive inductive reasoning which establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in all possible cases. An unproven proposition that is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for further mathematical work.

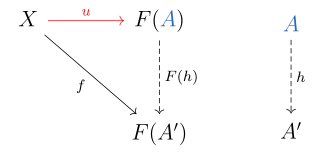
In category theory, a branch of mathematics, a universal property is an important property which is satisfied by a universal morphism. Universal morphisms can also be thought of more abstractly as initial or terminal objects of a comma category. Universal properties occur almost everywhere in mathematics, and hence the precise category theoretic concept helps point out similarities between different branches of mathematics, some of which may even seem unrelated.

In mathematics, two varying quantities are said to be in a relation of proportionality, multiplicatively connected to a constant; that is, when either their ratio or their product yields a constant. The value of this constant is called the coefficient of proportionality or proportionality constant.If the ratio of two variables is equal to a constant (k = y/x), then the variable in the numerator of the ratio can be product of the other variable and the constant (y = k ⋅ x). In this case y is said to be directly proportional to x with proportionality constant k. Equivalently one may write x = 1/k ⋅ y; that is, x is directly proportional to y with proportionality constant 1/k . If the term proportional is connected to two variables without further qualification, generally direct proportionality can be assumed. If the product of two variables (x ⋅ y) is equal to a constant (k = x ⋅ y), then the two are said to be inversely proportional to each other with the proportionality constant k. Equivalently, both variables are directly proportional to the reciprocal of the respective other with proportionality constant k.

In mathematics, the sign of a real number is its property of being either positive, negative, or zero. Depending on local conventions, zero may be considered as being neither positive nor negative, or it may be considered both positive and negative. Whenever not specifically mentioned, this article adheres to the first convention.

In mathematics, a space is a set with some added structure.

In mathematics, a theorem is a statement that has been proved, or can be proved. The proof of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of the axioms and previously proved theorems.

Two mathematical objects a and b are called equal up to an equivalence relation Rif a and b are related by R, that is, if aRb holds, that is, if the equivalence classes of a and b with respect to R are equal.