54 Symmetry

Symmetry in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including translation, reflection, rotation or scaling. Although these two meanings of "symmetry" can sometimes be told apart, they are intricately related, and hence are discussed together in this article.

Asymmetry is the absence of, or a violation of, symmetry. Symmetry is an important property of both physical and abstract systems and it may be displayed in precise terms or in more aesthetic terms. The absence of or violation of symmetry that are either expected or desired can have important consequences for a system.

The Ambidextrous Universe is a popular science book by Martin Gardner, covering aspects of symmetry and asymmetry in human culture, science and the wider universe.

In crystallography, a point group which contains an inversion center as one of its symmetry elements is centrosymmetric. In such a point group, for every point in the unit cell there is an indistinguishable point. Such point groups are also said to have inversion symmetry. Point reflection is a similar term used in geometry. Crystals with an inversion center cannot display certain properties, such as the piezoelectric effect.

In geometry, circular symmetry is a type of continuous symmetry for a planar object that can be rotated by any arbitrary angle and map onto itself.

In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name of the property that says "3 + 4 = 4 + 3" or "2 × 5 = 5 × 2", the property can also be used in more advanced settings. The name is needed because there are operations, such as division and subtraction, that do not have it ; such operations are not commutative, and so are referred to as noncommutative operations. The idea that simple operations, such as the multiplication and addition of numbers, are commutative was for many years implicitly assumed. Thus, this property was not named until the 19th century, when mathematics started to become formalized. A corresponding property exists for binary relations; a binary relation is said to be symmetric if the relation applies regardless of the order of its operands; for example, equality is symmetric as two equal mathematical objects are equal regardless of their order.

Confronted animals, or confronted-animal as an adjective, where two animals face each other in a symmetrical pose, is an ancient bilateral motif in art and artifacts studied in archaeology and art history. The "anti-confronted animals" is the opposing motif, with the animals back to back.

In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter, and has been more comprehensively defined by Norman Johnson.

In particle physics, CP violation is a violation of CP-symmetry : the combination of C-symmetry and P-symmetry. CP-symmetry states that the laws of physics should be the same if a particle is interchanged with its antiparticle while its spatial coordinates are inverted. The discovery of CP violation in 1964 in the decays of neutral kaons resulted in the Nobel Prize in Physics in 1980 for its discoverers James Cronin and Val Fitch.

In crystallography, the terms crystal system, crystal family, and lattice system each refer to one of several classes of space groups, lattices, point groups, or crystals. Informally, two crystals are in the same crystal system if they have similar symmetries, although there are many exceptions to this.

In three dimensional geometry, there are four infinite series of point groups in three dimensions (n≥1) with n-fold rotational or reflectional symmetry about one axis that does not change the object.

Cymatics is a subset of modal vibrational phenomena. The term was coined by Hans Jenny (1904-1972), a Swiss follower of the philosophical school known as anthroposophy. Typically the surface of a plate, diaphragm, or membrane is vibrated, and regions of maximum and minimum displacement are made visible in a thin coating of particles, paste, or liquid. Different patterns emerge in the excitatory medium depending on the geometry of the plate and the driving frequency.

The Droste effect, known in art as an example of mise en abyme, is the effect of a picture recursively appearing within itself, in a place where a similar picture would realistically be expected to appear, creating a loop which theoretically could go on forever, but realistically only goes on as far as the image's quality allows.

Jay Hambidge (1867–1924) was a Canadian-born American artist who formulated the theory of "dynamic symmetry", a system defining compositional rules, which was adopted by several notable American and Canadian artists in the early 20th century.

Facial symmetry is one specific measure of bodily symmetry. Along with traits such as averageness and youthfulness it influences judgments of aesthetic traits of physical attractiveness and beauty. For instance, in mate selection, people have been shown to have a preference for symmetry.

A gauge theory is a type of theory in physics. The word gauge means a measurement, a thickness, an in-between distance, or a resulting number of units per certain parameter. Modern theories describe physical forces in terms of fields, e.g., the electromagnetic field, the gravitational field, and fields that describe forces between the elementary particles. A general feature of these field theories is that the fundamental fields cannot be directly measured; however, some associated quantities can be measured, such as charges, energies, and velocities. For example, say you cannot measure the diameter of a lead ball, but you can determine how many lead balls, which are equal in every way, are required to make a pound. Using the number of balls, the elemental mass of lead, and the formula for calculating the volume of a sphere from its diameter, one could indirectly determine the diameter of a single lead ball. In field theories, different configurations of the unobservable fields can result in identical observable quantities. A transformation from one such field configuration to another is called a gauge transformation; the lack of change in the measurable quantities, despite the field being transformed, is a property called gauge invariance. For example, if you could measure the color of lead balls and discover that when you change the color, you still fit the same number of balls in a pound, the property of "color" would show gauge invariance. Since any kind of invariance under a field transformation is considered a symmetry, gauge invariance is sometimes called gauge symmetry. Generally, any theory that has the property of gauge invariance is considered a gauge theory.

In mathematics, a geometric transformation is any bijection of a set to itself with some salient geometrical underpinning. More specifically, it is a function whose domain and range are sets of points — most often both or both — such that the function is injective so that its inverse exists. The study of geometry may be approached via the study of these transformations.

In mathematics, a group is a set equipped with a binary operation that combines any two elements to form a third element in such a way that four conditions called group axioms are satisfied, namely closure, associativity, identity and invertibility. One of the most familiar examples of a group is the set of integers together with the addition operation, but groups are encountered in numerous areas within and outside mathematics, and help focusing on essential structural aspects, by detaching them from the concrete nature of the subject of the study.

In mathematics, a group action on a space is a group homomorphism of a given group into the group of transformations of the space. Similarly, a group action on a mathematical structure is a group homomorphism of a group into the automorphism group of the structure. It is said that the group acts on the space or structure. If a group acts on a structure, it will usually also act on objects built from that structure. For example, the group of Euclidean isometries acts on Euclidean space and also on the figures drawn in it. In particular, it acts on the set of all triangles. Similarly, the group of symmetries of a polyhedron acts on the vertices, the edges, and the faces of the polyhedron.

A gul is a medallion-like design element typical of traditional hand-woven carpets from Central and West Asia. In Turkmen weavings they are often repeated to form the pattern in the main field.

In the Standard Model of particle physics, the Higgs mechanism is essential to explain the generation mechanism of the property "mass" for gauge bosons. Without the Higgs mechanism, all bosons (one of the two classes of particles, the other being fermions) would be considered massless, but measurements show that the W+, W−, and Z0 bosons actually have relatively large masses of around 80 GeV/c2. The Higgs field resolves this conundrum. The simplest description of the mechanism adds a quantum field (the Higgs field) that permeates all space to the Standard Model. Below some extremely high temperature, the field causes spontaneous symmetry breaking during interactions. The breaking of symmetry triggers the Higgs mechanism, causing the bosons it interacts with to have mass. In the Standard Model, the phrase "Higgs mechanism" refers specifically to the generation of masses for the W±, and Z weak gauge bosons through electroweak symmetry breaking. The Large Hadron Collider at CERN announced results consistent with the Higgs particle on 14 March 2013, making it extremely likely that the field, or one like it, exists, and explaining how the Higgs mechanism takes place in nature.

Homological mirror symmetry is a mathematical conjecture made by Maxim Kontsevich. It seeks a systematic mathematical explanation for a phenomenon called mirror symmetry first observed by physicists studying string theory.

In mathematics, specifically in the representation theory of groups and algebras, an irreducible representation or irrep of an algebraic structure is a nonzero representation that has no proper nontrivial subrepresentation , with closed under the action of .

In mathematics, an isometry is a distance-preserving transformation between metric spaces, usually assumed to be bijective.

In mathematics, a Lie group is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract, generic concept of multiplication and the taking of inverses (division). Combining these two ideas, one obtains a continuous group where points can be multiplied together, and their inverse can be taken. If, in addition, the multiplication and taking of inverses are defined to be smooth (differentiable), one obtains a Lie group.

Towards the end of the nineteenth century, Sophus Lie introduced the notion of Lie group in order to study the solutions of ordinary differential equations (ODEs). He showed the following main property: the order of an ordinary differential equation can be reduced by one if it is invariant under one-parameter Lie group of point transformations. This observation unified and extended the available integration techniques. Lie devoted the remainder of his mathematical career to developing these continuous groups that have now an impact on many areas of mathematically based sciences. The applications of Lie groups to differential systems were mainly established by Lie and Emmy Noether, and then advocated by Élie Cartan.

Molecular symmetry in chemistry describes the symmetry present in molecules and the classification of molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can be used to predict or explain many of a molecule's chemical properties, such as its dipole moment and its allowed spectroscopic transitions.To do this it is necessary to classify the states of the molecule using the irreducible representations from the character table of the symmetry group of the molecule. Many university level textbooks on physical chemistry, quantum chemistry, spectroscopy and inorganic chemistry devote a chapter to symmetry.

Noether's theorem or Noether's first theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by mathematician Emmy Noether in 1915 and published in 1918, after a special case was proven by E. Cosserat and F. Cosserat in 1909. The action of a physical system is the integral over time of a Lagrangian function, from which the system's behavior can be determined by the principle of least action. This theorem only applies to continuous and smooth symmetries over physical space.

The Poincaré group, named after Henri Poincaré (1906), was first defined by Hermann Minkowski (1908) as the group of Minkowski spacetime isometries. It is a ten-dimensional non-abelian Lie group, which is of importance as a model in our understanding the most basic fundamentals of physics. For example, in one way of rigorously defining exactly what a subatomic particle is, Sheldon Lee Glashow has expressed that "Particles are at a very minimum described by irreducible representations of the Poincaré group."

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n.

Rotational symmetry, also known as radial symmetry in biology, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation.

The term sauwastika, सौवस्तिक In Devanagari script, is sometimes used to distinguish the left-facing from the right-facing swastika symbol, a meaning which developed in 19th-century scholarship.

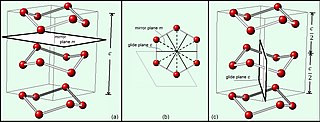
A screw axis is a line that is simultaneously the axis of rotation and the line along which translation of a body occurs. Chasles' theorem shows that each Euclidean displacement in three-dimensional space has a screw axis, and the displacement can be decomposed into a rotation about and a slide along this screw axis.

In mathematics, physics and chemistry, a space group is the symmetry group of a configuration in space, usually in three dimensions. In three dimensions, there are 219 distinct types, or 230 if chiral copies are considered distinct. Space groups are also studied in dimensions other than 3 where they are sometimes called Bieberbach groups, and are discrete cocompact groups of isometries of an oriented Euclidean space.

Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state ends up in an asymmetric state. In particular, it can describe systems where the equations of motion or the Lagrangian obey symmetries, but the lowest-energy vacuum solutions do not exhibit that same symmetry. When the system goes to one of those vacuum solutions, the symmetry is broken for perturbations around that vacuum even though the entire Lagrangian retains that symmetry.

In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group defined over a finite set of symbols consists of the permutations that can be performed on the symbols. Since there are such permutation operations, the order of the symmetric group is .

In geometry, an object has symmetry if there is an operation or transformation that maps the figure/object onto itself. Thus, a symmetry can be thought of as an immunity to change. For instance, a circle rotated about its center will have the same shape and size as the original circle, as all points before and after the transform would be indistinguishable. A circle is thus said to be symmetric under rotation or to have rotational symmetry. If the isometry is the reflection of a plane figure about a line, then the figure is said to have reflectional symmetry or line symmetry; it is also possible for a figure/object to have more than one line of symmetry.

In physics, symmetry breaking is a phenomenon in which (infinitesimally) small fluctuations acting on a system crossing a critical point decide the system's fate, by determining which branch of a bifurcation is taken. To an outside observer unaware of the fluctuations, the choice will appear arbitrary. This process is called symmetry "breaking", because such transitions usually bring the system from a symmetric but disorderly state into one or more definite states. Symmetry breaking is thought to play a major role in pattern formation.

In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).

Symmetry in biology refers to the symmetry observed in organisms, including plants, animals, fungi, and bacteria. External symmetry can be easily seen by just looking at an organism. For example, take the face of a human being which has a plane of symmetry down its centre, or a pine cone with a clear symmetrical spiral pattern. Internal features can also show symmetry, for example the tubes in the human body which are cylindrical and have several planes of symmetry.

Symmetry occurs not only in geometry, but also in other branches of mathematics. Symmetry is a type of invariance: the property that a mathematical object remains unchanged under a set of operations or transformations.

In physics, a symmetry of a physical system is a physical or mathematical feature of the system that is preserved or remains unchanged under some transformation.

The symmetry number or symmetry order of an object is the number of different but indistinguishable arrangements of the object, i.e. the order of its symmetry group. The object can be a molecule, crystal lattice, lattice, tiling, or in a general case any mathematical object in N-dimensions.

The SYZ conjecture is an attempt to understand the mirror symmetry conjecture, an issue in theoretical physics and mathematics. The original conjecture was proposed in a paper by Strominger, Yau, and Zaslow, entitled "Mirror Symmetry is T-duality".

T-symmetry or time reversal symmetry is the theoretical symmetry of physical laws under the transformation of time reversal,

Tendril perversion, often referred to in context as simply perversion, is a geometric phenomenon found in helical structures such as plant tendrils, in which a helical structure forms that is divided into two sections of opposite chirality, with a transition between the two in the middle. A similar phenomenon can often be observed in kinked helical cables such as telephone handset cords.

A tiling or tessellation of a flat surface is the covering of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellations can be generalized to higher dimensions and a variety of geometries.

Time translation symmetry or temporal translation symmetry (TTS) is a mathematical transformation in physics that moves the times of events through a common interval. Time translation symmetry is the hypothesis that the laws of physics are unchanged, under such a transformation. Time translation symmetry is a rigorous way to formulate the idea that the laws of physics are the same throughout history. Time translation symmetry is closely connected, via the Noether theorem, to conservation of energy. In mathematics, the set of all time translations on a given system form a Lie group.

In mathematics, transformation geometry is the name of a mathematical and pedagogic take on the study of geometry by focusing on groups of geometric transformations, and properties that are invariant under them. It is opposed to the classical synthetic geometry approach of Euclidean geometry, that focuses on proving theorems.

In geometry, to translate a geometric figure is to move it from one place to another without rotating it. A translation "slides" a thing by a: Ta(p) = p + a.

A triptych is a work of art that is divided into three sections, or three carved panels that are hinged together and can be folded shut or displayed open. It is therefore a type of polyptych, the term for all multi-panel works. The middle panel is typically the largest and it is flanked by two smaller related works, although there are triptychs of equal-sized panels. The form can also be used for pendant jewelry.

A triskelion or triskeles is a motif consisting of a triple spiral exhibiting rotational symmetry. The spiral design can be based on interlocking Archimedean spirals, or represent three bent human legs.

Yang–Mills theory is a gauge theory based on a special unitary group SU(N ), or more generally any compact, reductive Lie algebra. Yang–Mills theory seeks to describe the behavior of elementary particles using these non-abelian Lie groups and is at the core of the unification of the electromagnetic force and weak forces as well as quantum chromodynamics, the theory of the strong force. Thus it forms the basis of our understanding of the Standard Model of particle physics.