51 Geometry

Geometry is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space that are related with distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a geometer.

This is a list of geometry topics, by Wikipedia page.Geometric shape covers standard terms for plane shapes

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry is one of the oldest mathematical sciences.

In mathematics and theoretical physics, an amplituhedron is a geometric structure introduced in 2013 by Nima Arkani-Hamed and Jaroslav Trnka. It enables simplified calculation of particle interactions in some quantum field theories. In planar N = 4 supersymmetric Yang–Mills theory, also equivalent to the perturbative topological B model string theory in twistor space, an amplituhedron is defined as a mathematical space known as the positive Grassmannian.

An auxiliary line is an extra line needed to complete a proof in plane geometry. Other common auxiliary constructs in elementary plane synthetic geometry are the helping circles.

A biconcave disc — also referred to as a discocyte — is a geometric shape resembling an oblate spheroid with two concavities on the top and on the bottom.

In physics, a Bragg plane is a plane in reciprocal space which bisects a reciprocal lattice vector, , at right angles. The Bragg plane is defined as part of the Von Laue condition for diffraction peaks in x-ray diffraction crystallography.

Cat's cradle is one of the oldest games in recorded human history, and involves creating various string figures, either individually or by passing a loop of string back and forth between two or more players. The true origin of the name is debated, though the first known reference is in The light of nature pursued by Abraham Tucker in 1768. The type of string, the specific figures, their order, and the names of the figures vary. Independent versions of this game have been found in indigenous cultures throughout the world, including in Africa, Eastern Asia, the Pacific Islands, Australia, the Americas, and the Arctic.

A catenoid is a type of surface, arising by rotating a catenary curve about an axis. It is a minimal surface, meaning that it occupies the least area when bounded by a closed space. It was formally described in 1744 by the mathematician Leonhard Euler.

In geometry, Cavalieri's principle, a modern implementation of the method of indivisibles, named after Bonaventura Cavalieri, is as follows:2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane. If every line parallel to these two lines intersects both regions in line segments of equal length, then the two regions have equal areas. 3-dimensional case: Suppose two regions in three-space (solids) are included between two parallel planes. If every plane parallel to these two planes intersects both regions in cross-sections of equal area, then the two regions have equal volumes.

In geometry, coaxial means that two or more three-dimensional linear forms share a common axis. Thus, it is concentric in three-dimensional, linear forms.

The coin rotation paradox is the counter-intuitive observation that, when one coin is rolled around the rim of another coin of equal size, the moving coin completes two full rotations after going all the way around the stationary coin.

In geometry, a corner-point grid is a tessellation of a Euclidean 3D volume where the base cell has 6 faces (hexahedron).

In geometry, the tests for congruence and similarity involve comparing corresponding sides and corresponding angles of polygons. In these tests, each side and each angle in one polygon is paired with a side or angle in the second polygon, taking care to preserve the order of adjacency.

Coxeter decompositions of hyperbolic polygons

A Coxeter decomposition of a polygon is a decomposition into a finite number of polygons in which any two sharing a side are reflections of each other along that side. Hyperbolic polygons are the analogues of Euclidean polygons in hyperbolic geometry. A hyperbolic n-gon is an area bounded by n segments, rays, or entire straight lines. The standard model for this geometry is the Poincaré disk model. A major difference between Euclidean and hyperbolic polygons is that the sum of internal angles of a hyperbolic polygon is not the same as Euclidean polygons. In particular, the sum of the angles of a hyperbolic triangle is less than 180 degrees.

In geometry, the Cramer–Castillon problem is a problem stated by the Swiss mathematician Gabriel Cramer solved by the Italian mathematician, resident in Berlin, Jean de Castillon in 1776.

In four-dimensional geometry, the cubinder is one way to generalise the 3D cylinder to 4D. Like the duocylinder and spherinder, it is also analogous to a cylinder in 3-space, which is the Cartesian product of a disk with a line segment.

In geometry, an equichordal point is a point defined relative to a convex plane curve such that all chords passing through the point are equal in length. Two common figures with equichordal points are the circle and the limaçon. It is impossible for a curve to have more than one equichordal point.

In mathematics, a finite subdivision rule is a recursive way of dividing a polygon or other two-dimensional shape into smaller and smaller pieces. Subdivision rules in a sense are generalizations of regular geometric fractals. Instead of repeating exactly the same design over and over, they have slight variations in each stage, allowing a richer structure while maintaining the elegant style of fractals. Subdivision rules have been used in architecture, biology, and computer science, as well as in the study of hyperbolic manifolds. Substitution tilings are a well-studied type of subdivision rule.

In mathematics, a geometric transformation is any bijection of a set to itself with some salient geometrical underpinning. More specifically, it is a function whose domain and range are sets of points — most often both or both — such that the function is injective so that its inverse exists. The study of geometry may be approached via the study of these transformations.

Geometry processing, or mesh processing, is an area of research that uses concepts from applied mathematics, computer science and engineering to design efficient algorithms for the acquisition, reconstruction, analysis, manipulation, simulation and transmission of complex 3D models. As the name implies, many of the concepts, data structures, and algorithms are directly analogous to signal processing and image processing. For example, where image smoothing might convolve an intensity signal with a blur kernel formed using the Laplace operator, geometric smoothing might be achieved by convolving a surface geometry with a blur kernel formed using the Laplace-Beltrami operator.

A geometry template is a piece of clear plastic with cut-out shapes for use in mathematics and other subjects in primary school through secondary school. It also has various measurements on its sides to be used like a ruler. In Australia, popular brands include Mathomat and MathAid.

A great ellipse is an ellipse passing through two points on a spheroid and having the same center as that of the spheroid. Equivalently, it is an ellipse on the surface of a spheroid and centered on the origin, or the curve formed by intersecting the spheroid by a plane through its center. For points that are separated by less than about a quarter of the circumference of the earth, about , the length of the great ellipse connecting the points is close to the geodesic distance. The great ellipse therefore is sometimes proposed as a suitable route for marine navigation. The great ellipse is special case of an earth section path.

Haruki's Theorem says that given three intersecting circles that only intersect each other at two points that the lines connecting the inner intersecting points to the outer satisfy:

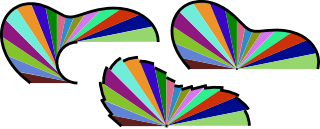
Lacunarity, from the Latin lacuna, meaning "gap" or "lake", is a specialized term in geometry referring to a measure of how patterns, especially fractals, fill space, where patterns having more or larger gaps generally have higher lacunarity. Beyond being an intuitive measure of gappiness, lacunarity can quantify additional features of patterns such as "rotational invariance" and more generally, heterogeneity. This is illustrated in Figure 1 showing three fractal patterns. When rotated 90°, the first two fairly homogeneous patterns do not appear to change, but the third more heterogeneous figure does change and has correspondingly higher lacunarity. The earliest reference to the term in geometry is usually attributed to Mandelbrot, who, in 1983 or perhaps as early as 1977, introduced it as, in essence, an adjunct to fractal analysis. Lacunarity analysis is now used to characterize patterns in a wide variety of fields and has application in multifractal analysis in particular.

In mathematics, a Laguerre plane is one of the Benz planes: the Möbius plane, Laguerre plane and Minkowski plane, named after the French mathematician Edmond Nicolas Laguerre.

A Lénárt sphere is a teaching and educational research model for spherical geometry. The Lénárt sphere is a modern replacement of a "spherical blackboard". It can be used for visualizing spherical polygons showing the relationships between the sides and the angles.

In Euclidean geometry, linear separability is a property of two sets of points. This is most easily visualized in two dimensions by thinking of one set of points as being colored blue and the other set of points as being colored red. These two sets are linearly separable if there exists at least one line in the plane with all of the blue points on one side of the line and all the red points on the other side. This idea immediately generalizes to higher-dimensional Euclidean spaces if the line is replaced by a hyperplane.

Mathematical phenomena can be understood and explored via visualization. Classically this consisted of two-dimensional drawings or building three-dimensional models, while today it most frequently consists of using computers to make static two or three dimensional drawings, animations, or interactive programs. Writing programs to visualize mathematics is an aspect of computational geometry.

Miller indices form a notation system in crystallography for planes in crystal (Bravais) lattices.

In geometry, the minimum or smallest bounding or enclosing box for a point set (S) in N dimensions is the box with the smallest measure within which all the points lie. When other kinds of measure are used, the minimum box is usually called accordingly, e.g., "minimum-perimeter bounding box".

In mathematical physics, Minkowski space is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be implied by the postulates of special relativity.

In mathematics, physics, and art, moiré patterns or moiré fringes are large-scale interference patterns that can be produced when an opaque ruled pattern with transparent gaps is overlaid on another similar pattern. For the moiré interference pattern to appear, the two patterns must not be completely identical, but rather displaced, rotated, or have slightly different pitch.

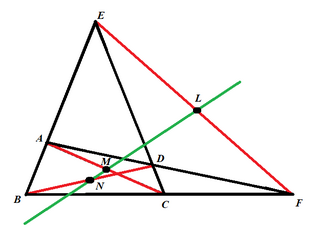
In geometry, the Newton–Gauss line is the line joining the midpoints of the three diagonals of a complete quadrangle.

In geometry, a nonagon or enneagon is a nine-sided polygon or 9-gon.

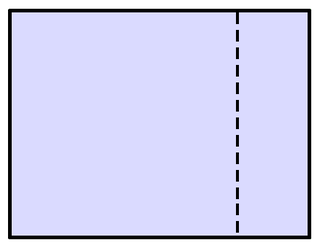
Rabatment of the rectangle is a compositional technique used as an aid for the placement of objects or the division of space within a rectangular frame, or as an aid for the study of art.

In three-dimensional space, a regulus R is a set of skew lines, every point of which is on a transversal which intersects an element of R only once, and such that every point on a transversal lies on a line of R

A secant plane is a plane containing a nontrivial section of a sphere or an ellipsoid, or such a plane that a sphere is projected onto. Secant planes are similar to tangent planes, which contact the sphere's surface at a point, while secant planes contact the surface along curves.

In mathematics, a sheaf of planes is the set of all planes that have the same common line. It may also be known as a pencil or fan of planes.

In geometry, a snub is an operation applied to a polyhedron. The term originates from Kepler's names of two Archimedean solids, for the snub cube and snub dodecahedron. In general, snubs have chiral symmetry with two forms: with clockwise or counterclockwise orientation. By Kepler's names, a snub can be seen as an expansion of a regular polyhedron: moving the faces apart, twisting them about their centers, adding new polygons centered on the original vertices, and adding pairs of triangles fitting between the original edges.

Space is the boundless three-dimensional extent in which objects and events have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum known as spacetime. The concept of space is considered to be of fundamental importance to an understanding of the physical universe. However, disagreement continues between philosophers over whether it is itself an entity, a relationship between entities, or part of a conceptual framework.

A spacetime diagram is a graphical illustration of the properties of space and time in the special theory of relativity. Spacetime diagrams allow a qualitative understanding of the corresponding phenomena like time dilation and length contraction without mathematical equations.

Strähle's construction is a geometric method for determining the lengths for a series of vibrating strings with uniform diameters and tensions to sound pitches in a specific rational tempered musical tuning. It was first published in the 1743 Proceedings of the Royal Swedish Academy of Sciences by Swedish master organ maker Daniel Stråhle (1700–1746). The Academy's secretary Jacob Faggot appended a miscalculated set of pitches to the article, and these figures were reproduced by Friedrich Wilhelm Marpurg in Versuch über die musikalische Temperatur in 1776. Several German textbooks published about 1800 reported that the mistake was first identified by Christlieb Benedikt Funk in 1779, but the construction itself appears to have received little notice until the middle of the twentieth century when tuning theorist J. Murray Barbour presented it as a good method for approximating equal temperament and similar exponentials of small roots, and generalized its underlying mathematical principles.

In mathematics, a subpaving is a set of nonoverlapping boxes of Rn. A subset X of Rn can be approximated by two subpavings X− and X+ such that X− ⊂ X ⊂ X+. The three figures on the right show an approximation of the set X = {(x1, x2) ∈ R2 | x12 + x22 + sin(x1 + x2) ∈ [4,9]} with different accuracies. The set X− corresponds to red boxes and the set X+ contains all red and yellow boxes.

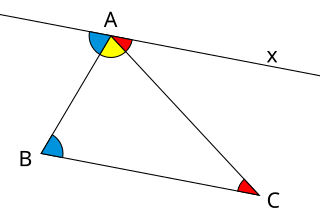
In a Euclidean space, the sum of angles of a triangle equals the straight angle . A triangle has three angles, one at each vertex, bounded by a pair of adjacent sides.

In mathematics, a surface is a generalization of a plane, which is not necessarily flat – that is, the curvature is not necessarily zero. This is analogous to a curve generalizing a straight line. There are many more precise definitions, depending on the context and the mathematical tools that are used to analyze the surface.

Symmetry in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including translation, reflection, rotation or scaling. Although these two meanings of "symmetry" can sometimes be told apart, they are intricately related, and hence are discussed together in this article.

In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).

In geometry, the unit hyperbola is the set of points (x,y) in the Cartesian plane that satisfy the implicit equation In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial length

Visual calculus, invented by Mamikon Mnatsakanian, is an approach to solving a variety of integral calculus problems. Many problems that would otherwise seem quite difficult yield to the method with hardly a line of calculation, often reminiscent of what Martin Gardner calls "aha! solutions" or Roger Nelsen a proof without words.

Wittgenstein's rod is a geometry problem discussed by 20th-century philosopher Ludwig Wittgenstein.