31 Control theory

The 4D/RCS Reference Model Architecture is a reference model for military unmanned vehicles on how their software components should be identified and organized.

The asymptotic gain model is a representation of the gain of negative feedback amplifiers given by the asymptotic gain relation:

Bicycle and motorcycle dynamics is the science of the motion of bicycles and motorcycles and their components, due to the forces acting on them. Dynamics falls under a branch of physics known as classical mechanics. Bike motions of interest include balancing, steering, braking, accelerating, suspension activation, and vibration. The study of these motions began in the late 19th century and continues today.

Bode's sensitivity integral, discovered by Hendrik Wade Bode, is a formula that quantifies some of the limitations in feedback control of linear parameter invariant systems. Let L be the loop transfer function and S be the sensitivity function.

A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large Industrial control systems which are used for controlling processes or machines.

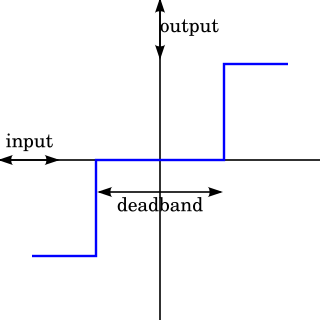
A deadband or dead-band is a band of input values in the domain of a transfer function in a control system or signal processing system where the output is zero. Deadband regions can be used in control systems such as servoamplifiers to prevent oscillation or repeated activation-deactivation cycles. A form of deadband that occurs in mechanical systems, compound machines such as gear trains is backlash.

In mathematics, delay differential equations (DDEs) are a type of differential equation in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times. DDEs are also called time-delay systems, systems with aftereffect or dead-time, hereditary systems, equations with deviating argument, or differential-difference equations. They belong to the class of systems with the functional state, i.e. partial differential equations (PDEs) which are infinite dimensional, as opposed to ordinary differential equations (ODEs) having a finite dimensional state vector. Four points may give a possible explanation of the popularity of DDEs:Aftereffect is an applied problem: it is well known that, together with the increasing expectations of dynamic performances, engineers need their models to behave more like the real process. Many processes include aftereffect phenomena in their inner dynamics. In addition, actuators, sensors, and communication networks that are now involved in feedback control loops introduce such delays. Finally, besides actual delays, time lags are frequently used to simplify very high order models. Then, the interest for DDEs keeps on growing in all scientific areas and, especially, in control engineering. Delay systems are still resistant to many classical controllers: one could think that the simplest approach would consist in replacing them by some finite-dimensional approximations. Unfortunately, ignoring effects which are adequately represented by DDEs is not a general alternative: in the best situation, it leads to the same degree of complexity in the control design. In worst cases, it is potentially disastrous in terms of stability and oscillations. Voluntary introduction of delays can benefit the control system. In spite of their complexity, DDEs often appear as simple infinite-dimensional models in the very complex area of partial differential equations (PDEs).

In applied mathematics, discretization is the process of transferring continuous functions, models, variables, and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers. Dichotomization is the special case of discretization in which the number of discrete classes is 2, which can approximate a continuous variable as a binary variable.

The falling cat problem is a problem that consists of explaining the underlying physics behind the observation of the cat righting reflex: that is, how a free-falling body can change its orientation such that it is able to right itself as it falls to land on its feet, irrespective of its initial orientation, and without violating the law of conservation of angular momentum.

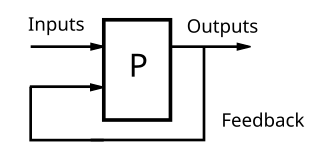
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause-and-effect that forms a circuit or loop. The system can then be said to feed back into itself. The notion of cause-and-effect has to be handled carefully when applied to feedback systems:Simple causal reasoning about a feedback system is difficult because the first system influences the second and second system influences the first, leading to a circular argument. This makes reasoning based upon cause and effect tricky, and it is necessary to analyze the system as a whole.

Hall circles are a graphical tool in control theory used to obtain values of a closed-loop transfer function from the Nyquist plot of the associated open-loop transfer function. Hall circles have been introduced in control theory by Albert C. Hall in his thesis.

A head-related transfer function (HRTF), also sometimes known as the anatomical transfer function (ATF), is a response that characterizes how an ear receives a sound from a point in space. As sound strikes the listener, the size and shape of the head, ears, ear canal, density of the head, size and shape of nasal and oral cavities, all transform the sound and affect how it is perceived, boosting some frequencies and attenuating others. Generally speaking, the HRTF boosts frequencies from 2–5 kHz with a primary resonance of +17 dB at 2,700 Hz. But the response curve is more complex than a single bump, affects a broad frequency spectrum, and varies significantly from person to person.

In signal processing, the impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response is the reaction of any dynamic system in response to some external change. In both cases, the impulse response describes the reaction of the system as a function of time.

In the study of mechanical networks in control theory, an inerter is a two-terminal device in which the forces applied at the terminals are equal, opposite, and proportional to relative acceleration between the nodes. Under the name of J-damper the concept has been used in Formula 1 racing car suspension systems.

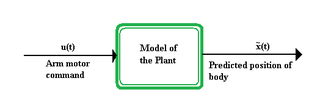
In the subject area of control theory, an internal model is a process that simulates the response of the system in order to estimate the outcome of a system disturbance. The internal model principle was first articulated in 1976 by B. A. Francis and W. M. Wonham as an explicit formulation of the Conant and Ashby good regulator theorem. It stands in contrast to classical control, in that the classical feedback loop fails to explicitly model the controlled system.

In statistics and control theory, Kalman filtering, also known as linear quadratic estimation (LQE), is an algorithm that uses a series of measurements observed over time, containing statistical noise and other inaccuracies, and produces estimates of unknown variables that tend to be more accurate than those based on a single measurement alone, by estimating a joint probability distribution over the variables for each timeframe. The filter is named after Rudolf E. Kálmán, one of the primary developers of its theory.

The matched Z-transform method, also called the pole–zero mapping or pole–zero matching method, and abbreviated MPZ or MZT, is a technique for converting a continuous-time filter design to a discrete-time filter design.

Motion control is a sub-field of automation, encompassing the systems or sub-systems involved in moving parts of machines in a controlled manner. A motion control system is extensively used in a variety of fields for automation purposes, including precision engineering, micromanufacturing, biotechnology, and nanotechnology. The main components involved typically include a motion controller, an energy amplifier, and one or more prime movers or actuators. Motion control may be open loop or closed loop. In open loop systems, the controller sends a command through the amplifier to the prime mover or actuator, and does not know if the desired motion was actually achieved. Typical systems include stepper motor or fan control. For tighter control with more precision, a measuring device may be added to the system. When the measurement is converted to a signal that is sent back to the controller, and the controller compensates for any error, it becomes a Closed loop System.

In control theory, multiple models is an approach to improve efficiency of adaptive system or observer system. It uses large number of models, which are distributed in the region of uncertainty, and based on the responses of the plant and the models. One model is chosen at every instant, which is closest to the plant according to some metric. The method offers satisfactory performance when no restrictions are put on the number of available models.

Negative feedback occurs when some function of the output of a system, process, or mechanism is fed back in a manner that tends to reduce the fluctuations in the output, whether caused by changes in the input or by other disturbances.

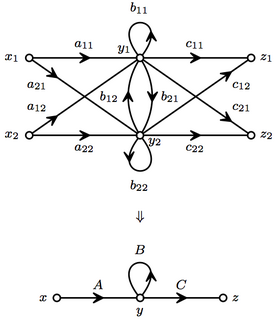
In automata theory and control theory, branches of mathematics, theoretical computer science and systems engineering, a noncommutative signal-flow graph is a tool for modeling interconnected systems and state machines by mapping the edges of a directed graph to a ring or semiring.

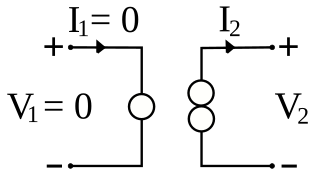
In electronics, a norator is a theoretical linear, time-invariant one-port which can have an arbitrary current and voltage between its terminals. A norator represents a controlled voltage or current source with infinite gain.

In electronics, a nullator is a theoretical linear, time-invariant one-port defined as having zero current and voltage across its terminals. Nullators are strange in the sense that they simultaneously have properties of both a short and an open circuit. They are neither current nor voltage sources, yet both at the same time.

A nullor is a theoretical two-port network consisting of a nullator at its input and a norator at its output. Nullors represent an ideal amplifier, having infinite current, voltage, transconductance and transimpedance gain. Its transmission parameters are all zero, that is, its input–output behavior is summarized with the matrix equation

Proportional control, in engineering and process control, is a type of linear feedback control system in which a correction is applied to the controlled variable which is proportional to the difference between the desired value and the measured value. Two classic mechanical examples are the toilet bowl float proportioning valve and the fly-ball governor.

Servos are small, cheap, mass-produced servomotors or other actuators used for radio control and small-scale robotics.

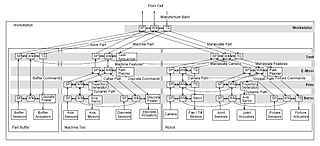
Real-time Control System (RCS) is a reference model architecture, suitable for many software-intensive, real-time computing control problem domains. It defines the types of functions needed in a real-time intelligent control system, and how these functions relate to each other.

In cybernetics and control theory, a setpoint is the desired or target value for an essential variable, or process value of a system. Departure of such a variable from its setpoint is one basis for error-controlled regulation using negative feedback for automatic control. The set point is usually abbreviated to SP, and the process value is usually abbreviated to PV.

The Smith predictor is a type of predictive controller designed to control systems with a significant feedback time delay. The idea can be illustrated as follows.

In electrical engineering and mechanical engineering, a transient response is the response of a system to a change from an equilibrium or a steady state. The transient response is not necessarily tied to abrupt events but to any event that affects the equilibrium of the system. The impulse response and step response are transient responses to a specific input.

Witsenhausen's counterexample, shown in the figure below, is a deceptively simple toy problem in decentralized stochastic control. It was formulated by Hans Witsenhausen in 1968. It is a counterexample to a natural conjecture that one can generalize a key result of centralized linear–quadratic–Gaussian control systems—that in a system with linear dynamics, Gaussian disturbance, and quadratic cost, affine (linear) control laws are optimal—to decentralized systems. Witsenhausen constructed a two-stage linear quadratic Gaussian system where two decisions are made by decision makers with decentralized information and showed that for this system, there exist nonlinear control laws that outperform all linear laws. The problem of finding the optimal control law remains unsolved.