27 Mathematical optimization

Mathematical optimization or mathematical programming is the selection of a best element from some set of available alternatives. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.

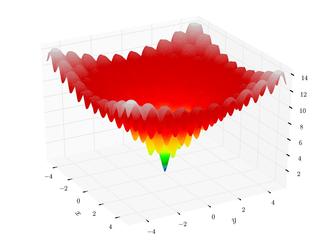
In mathematical optimization, the Ackley function is a non-convex function used as a performance test problem for optimization algorithms. It was proposed by David Ackley in his 1987 PhD Dissertation.

Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models.

In mathematics, the cake number, denoted by Cn, is the maximum number of regions into which a 3-dimensional cube can be partitioned by exactly n planes. The cake number is so-called because one may imagine each partition of the cube by a plane as a slice made by a knife through a cube-shaped cake.

Dispersive flies optimisation (DFO) is a bare-bones swarm intelligence algorithm which is inspired by the swarming behaviour of flies hovering over food sources. DFO is a simple optimiser which works by iteratively trying to improve a candidate solution with regard to a numerical measure that is calculated by a fitness function. Each member of the population, a fly or an agent, holds a candidate solution whose suitability can be evaluated by their fitness value. Optimisation problems are often formulated as either minimisation or maximisation problems.

In mathematics, a knee of a curve is a point where the curve visibly bends, specifically from high slope to low slope, or in the other direction. This is particularly used in optimization, where a knee point is the optimum point for some decision, for example when there is an increasing function and a trade-off between the benefit and the cost : the knee is where the benefit is no longer increasing rapidly, and is no longer worth the cost of further increases – a cutoff point of diminishing returns.

In mathematical optimization, a feasible region, feasible set, search space, or solution space is the set of all possible points of an optimization problem that satisfy the problem's constraints, potentially including inequalities, equalities, and integer constraints. This is the initial set of candidate solutions to the problem, before the set of candidates has been narrowed down.

The geometric median of a discrete set of sample points in a Euclidean space is the point minimizing the sum of distances to the sample points. This generalizes the median, which has the property of minimizing the sum of distances for one-dimensional data, and provides a central tendency in higher dimensions. It is also known as the 1-median, spatial median, Euclidean minisum point, or Torricelli point.

In mathematical optimization, Himmelblau's function is a multi-modal function, used to test the performance of optimization algorithms. The function is defined by:

In mathematics, a knee of a curve is a point where the curve visibly bends, specifically from high slope to low slope, or in the other direction. This is particularly used in optimization, where a knee point is the optimum point for some decision, for example when there is an increasing function and a trade-off between the benefit and the cost : the knee is where the benefit is no longer increasing rapidly, and is no longer worth the cost of further increases – a cutoff point of diminishing returns.

The lazy caterer's sequence, more formally known as the central polygonal numbers, describes the maximum number of pieces of a disk that can be made with a given number of straight cuts. For example, three cuts across a pancake will produce six pieces if the cuts all meet at a common point inside the circle, but up to seven if they do not. This problem can be formalized mathematically as one of counting the cells in an arrangement of lines; for generalizations to higher dimensions, see arrangement of hyperplanes.

In applied mathematics and computer science, a local optimum of an optimization problem is a solution that is optimal within a neighboring set of candidate solutions. This is in contrast to a global optimum, which is the optimal solution among all possible solutions, not just those in a particular neighborhood of values.

In mathematical analysis, the maxima and minima of a function, known collectively as extrema, are the largest and smallest value of the function, either within a given range, or on the entire domain. Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions.

Multiple-criteria decision-making (MCDM) or multiple-criteria decision analysis (MCDA) is a sub-discipline of operations research that explicitly evaluates multiple conflicting criteria in decision making. Conflicting criteria are typical in evaluating options: cost or price is usually one of the main criteria, and some measure of quality is typically another criterion, easily in conflict with the cost. In purchasing a car, cost, comfort, safety, and fuel economy may be some of the main criteria we consider – it is unusual that the cheapest car is the most comfortable and the safest one. In portfolio management, managers are interested in getting high returns while simultaneously reducing risks; however, the stocks that have the potential of bringing high returns typically carry high risk of losing money. In a service industry, customer satisfaction and the cost of providing service are fundamental conflicting criteria.

In computational complexity and optimization the no free lunch theorem is a result that states that for certain types of mathematical problems, the computational cost of finding a solution, averaged over all problems in the class, is the same for any solution method. No solution therefore offers a "short cut". This is under the assumption that the search space is a probability density function. It does not apply to the case where the search space has underlying structure that can be exploited more efficiently than random search or even has closed-form solutions that can be determined without search at all. For such probabilistic assumptions, the outputs of all procedures solving a particular type of problem are statistically identical. A colourful way of describing such a circumstance, introduced by David Wolpert and William G. Macready in connection with the problems of search and optimization, is to say that there is no free lunch. Wolpert had previously derived no free lunch theorems for machine learning. Before Wolpert's article was published, Cullen Schaffer independently proved a restricted version of one of Wolpert's theorems and used it to critique the current state of machine learning research on the problem of induction.

In computational complexity theory, a problem is NP-complete when:A nondeterministic Turing machine can solve it in polynomial-time. A deterministic Turing machine can solve it in large time complexity classes and can verify its solutions in polynomial time. It can be used to simulate any other problem with similar solvability.

In the design of experiments, optimal designs are a class of experimental designs that are optimal with respect to some statistical criterion. The creation of this field of statistics has been credited to Danish statistician Kirstine Smith.

The P versus NP problem is a major unsolved problem in computer science. It asks whether every problem whose solution can be quickly verified can also be solved quickly.

In geometry, the paper bag problem or teabag problem is to calculate the maximum possible inflated volume of an initially flat sealed rectangular bag which has the same shape as a cushion or pillow, made out of two pieces of material which can bend but not stretch.

In mathematical optimization, the Rastrigin function is a non-convex function used as a performance test problem for optimization algorithms. It is a typical example of non-linear multimodal function. It was first proposed in 1974 by Rastrigin as a 2-dimensional function and has been generalized by Rudolph. The generalized version was popularized by Hoffmeister & Bäck and Mühlenbein et al. Finding the minimum of this function is a fairly difficult problem due to its large search space and its large number of local minima.

In statistics, response surface methodology (RSM) explores the relationships between several explanatory variables and one or more response variables. The method was introduced by George E. P. Box and K. B. Wilson in 1951. The main idea of RSM is to use a sequence of designed experiments to obtain an optimal response. Box and Wilson suggest using a second-degree polynomial model to do this. They acknowledge that this model is only an approximation, but they use it because such a model is easy to estimate and apply, even when little is known about the process.

In mathematical optimization, the Rosenbrock function is a non-convex function, introduced by Howard H. Rosenbrock in 1960, which is used as a performance test problem for optimization algorithms. It is also known as Rosenbrock's valley or Rosenbrock's banana function.

Shekel function is a multidimensional, multimodal, continuous, deterministic function commonly used as a test function for testing optimization techniques.

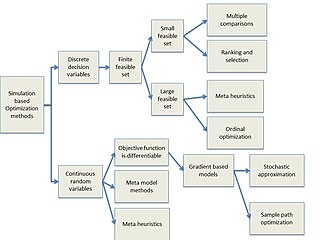
Simulation-based optimization integrates optimization techniques into simulation modeling and analysis. Because of the complexity of the simulation, the objective function may become difficult and expensive to evaluate. Usually, the underlying simulation model is stochastic, so that that the objective function must be estimated using statistical estimation techniques.

In theoretical computer science, smoothed analysis is a way of measuring the complexity of an algorithm. Since its introduction in 2001, smoothed analysis has been used as a basis for considerable research, for problems ranging from mathematical programming, numerical analysis, machine learning, and data mining. It can give a more realistic analysis of the practical performance of the algorithm, such as its running time, than using worst-case or average-case scenarios.

Steiner's problem, asked and answered by Steiner (1850), is the problem of finding the maximum of the function