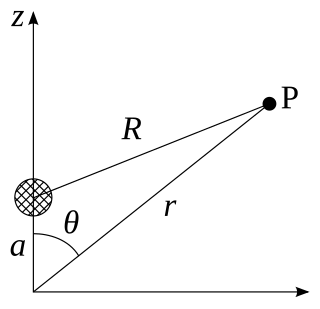
 W
WAxial multipole moments are a series expansion of the electric potential of a charge distribution localized close to the origin along one Cartesian axis, denoted here as the z-axis. However, the axial multipole expansion can also be applied to any potential or field that varies inversely with the distance to the source, i.e., as . For clarity, we first illustrate the expansion for a single point charge, then generalize to an arbitrary charge density localized to the z-axis.
 W
WIn electromagnetism, there are two kinds of dipoles:An electric dipole deals with the separation of the positive and negative charges found in any electromagnetic system. A simple example of this system is a pair of electric charges of equal magnitude but opposite sign separated by some typically small distance. A magnetic dipole is the closed circulation of an electric current system. A simple example is a single loop of wire with constant current through it. A bar magnet is an example of a magnet with a permanent magnetic dipole moment.
 W
WAn Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism is a fundamental publication by George Green in 1828, where he extends previous work of Siméon Denis Poisson on electricity and magnetism. The work in mathematical analysis, notably including what is now universally known as Green's theorem, is of the greatest importance in all branches of mathematical physics. It contains the first exposition of the theory of potential. In physics, Green's theorem is mostly used to solve two-dimensional flow integrals, stating that the sum of fluid outflows at any point inside a volume is equal to the total outflow summed about an enclosing area. In plane geometry, and in particular, area surveying, Green's theorem can be used to determine the area and centroid of plane figures solely by integrating over the perimeter.
 W
WIn geometry, a focaloid is a shell bounded by two concentric, confocal ellipses or ellipsoids (in 3D). When the thickness of the shell becomes negligible, it is called a thin focaloid.
 W
WIn mathematics, especially potential theory, harmonic measure is a concept related to the theory of harmonic functions that arises from the solution of the classical Dirichlet problem.
 W
WPoisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with the potential field known, one can then calculate electrostatic or gravitational (force) field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after French mathematician and physicist Siméon Denis Poisson.
 W
WA potential energy surface (PES) describes the energy of a system, especially a collection of atoms, in terms of certain parameters, normally the positions of the atoms. The surface might define the energy as a function of one or more coordinates; if there is only one coordinate, the surface is called a potential energy curve or energy profile. An example is the Morse/Long-range potential.